Introduction
In previous posts I have introduced dynamic integration techniques, MVC designs, Kotlin and TornadoFX. It is now time to put all the pieces together in a free-standing app with a responsive user interface. The final result will look like these two screen shots.
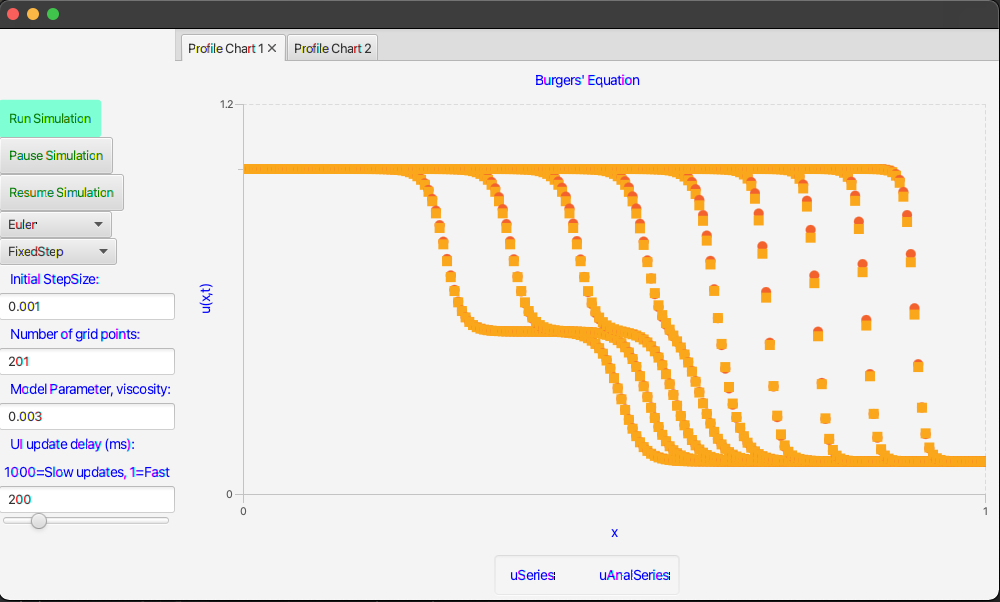
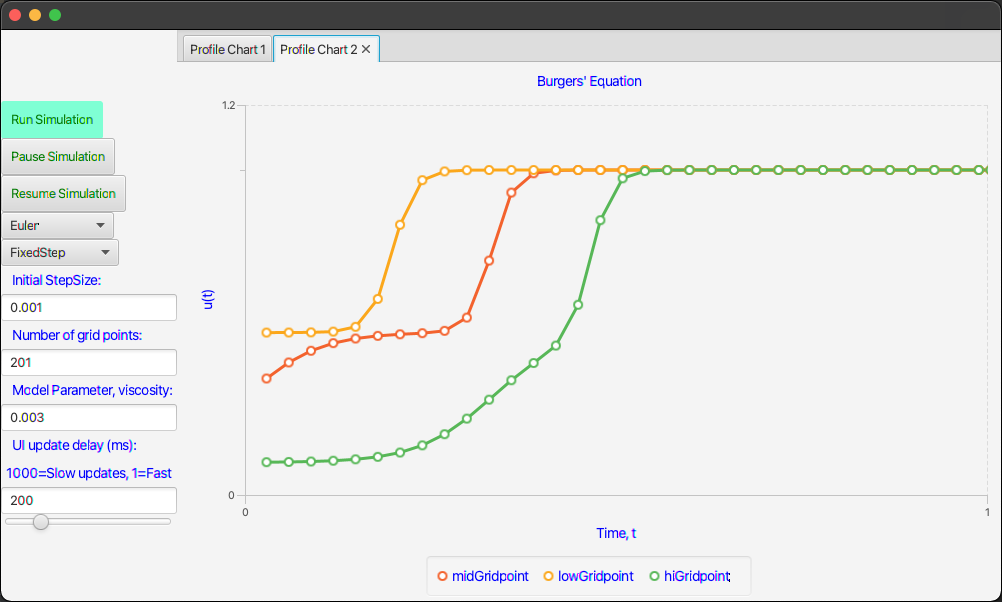
Let’s get started putting this app together piece by piece.
Create the Project Template
In previous posts I have shown how to do this so I will move quickly through this section.
Step 1. Make a new project with JetBrains IntelliJ.
Step 2. Link the project to any local, supporting projects you might have (in my case SyMods), assign dependencies in build.gradle and finally provide empty folders (packages) for the “app”, “model”, “view” and the “controller” as in MVC.
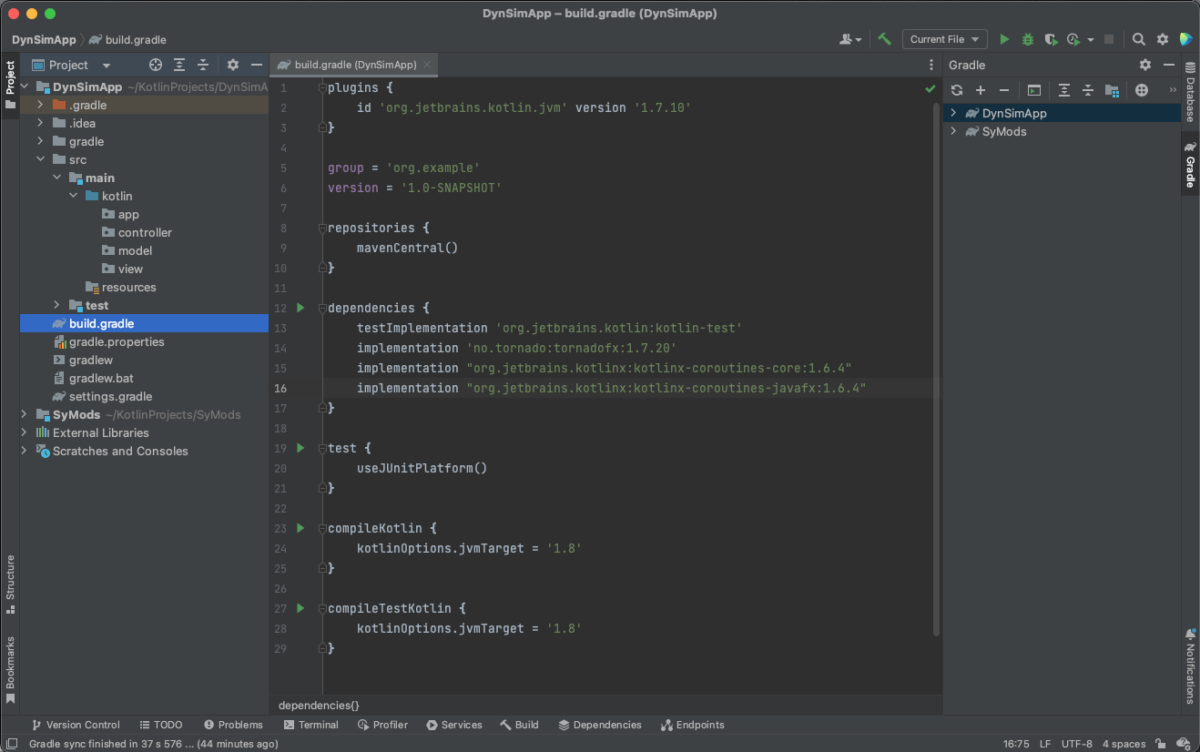
Since the build.gradle is such an important part of the project I show the script more clearly here:
plugins {
id 'org.jetbrains.kotlin.jvm' version '1.7.10'
}
group = 'org.example'
version = '1.0-SNAPSHOT'
repositories {
mavenCentral()
}
dependencies {
testImplementation 'org.jetbrains.kotlin:kotlin-test'
implementation 'org.example:SyMods'
implementation 'no.tornado:tornadofx:1.7.20'
implementation "org.jetbrains.kotlinx:kotlinx-coroutines-core:1.6.4"
implementation "org.jetbrains.kotlinx:kotlinx-coroutines-javafx:1.6.4"
}
test {
useJUnitPlatform()
}
compileKotlin {
kotlinOptions.jvmTarget = '1.8'
}
compileTestKotlin {
kotlinOptions.jvmTarget = '1.8'
}The Model
In most versions of MVC designs, the model is the only part that is completely independent of the other pieces. In other words, the model has no knowledge of either the view or the (view-) controller. The only contract the model has with the outside world is that it implements the Integratable interface. That way the same model, without substantial modifications, can be used with a completely different user interface implementation (e.g. Java/Swing or Swift/Cocoa).
The model I have chosen for this example is borrowed from the field of fluid dynamics. Such systems are described by a set of nonlinear partial differential equations expressing the conservation of mass and momentum for incompressible Newtonian fluids. The fluid velocity in three dimensions is captured in the Navier Stokes equation of fluid dynamics (see Ref. 1 for a complete derivation).
If we limit the flow model to the fluid velocity component in one dimension, and neglect pressure and gravitational effects, we obtain the one-dimensional Burgers’ equation.
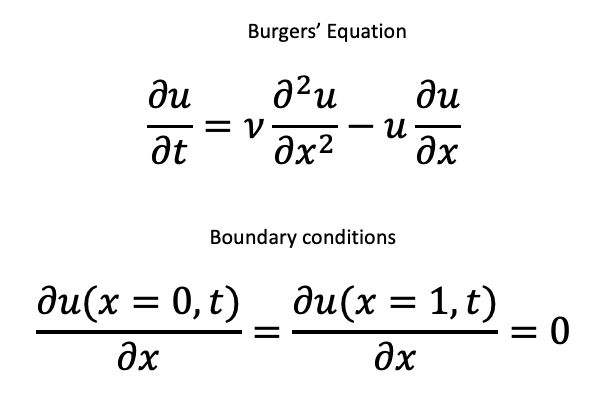
We can think of this equation as representing the velocity in the x-direction as the fluid is moving freely along a path. Note that the fluid is viscous as captured by the kinematic viscosity, v (m^2/s).
According to Ref. 1, Burgers’ equation is a standard test problem for numerical methods for two reasons (1) It is a nonlinear equation with known analytical solutions, (2) It can be made increasingly more difficult to solve numerically as the viscosity decreases.
The equation is first order in time and second order in space. Thus, it requires one initial condition and two boundary conditions. The initial condition is taken from the analytical solution at time = 0. The boundary conditions are shown above. They state that the spatial velocity derivative is zero at both ends of the flow path at all times.
Numerical techniques for solving partial differential equations like this typically involve breaking up the x-direction in a large number (N-1) of small segments, dx, flanked by N grid points to help with the approximation of the spatial derivatives. This way we end up with a set of N ordinary differential equations that can be solved with standard integrators such as Euler or Runge-Kutta.
For this example I’m choosing to use a Spline Collocation Method to approximate the first and second order spatial derivatives (See Ref. 2 for details of this method). The complete code for the model is shown here:
package model
import integrators.Integratable
import utilities.derivativesAtGridpoints
import kotlin.math.exp
class BurgersEquation(var nGridPoints: Int): Integratable {
val length = 1.0
var dx = length / (nGridPoints - 1)
var time = 0.0
var vis = 0.003
var x = DoubleArray(nGridPoints) { it * dx }
var u = DoubleArray(nGridPoints) { phi(x[it], time) }
override fun initialConditionsUsingArray(xin: DoubleArray): DoubleArray {
x = DoubleArray(nGridPoints) { it * dx }
val u0 = xin.copyOf()
for (i in 0 until nGridPoints) {
u0[i] = phi(this.x[i], time)
}
return u0
}
override fun updateStatesFromStateVector(x: DoubleArray, time: Double) {
this.time = time
u = x
}
override fun updateDerivativeVector(df: DoubleArray, time: Double): DoubleArray {
val ux = derivativesAtGridpoints(xL=0.0, xU=length, n=nGridPoints, u=u).b
ux[0] = 0.0
ux[nGridPoints-1] = 0.0
val uxx = derivativesAtGridpoints(xL=0.0, xU=length, n=nGridPoints, u=ux).b
val ut = df.copyOf()
for (i in 0 until nGridPoints) {
ut[i] = vis * uxx[i] - u[i] * ux[i]
}
return ut
}
override fun dimension(): Int {
return nGridPoints
}
override fun stiff(): Boolean {
return false
}
fun phi(x: Double, t: Double): Double {
//
// Function phi computes the exact solution of Burgers' equation
// for comparison with the numerical solution. It is also used to
// define the initial and boundary conditions for the numerical
// solution.
//
// Analytical solution
val a = (0.05 / vis) * (x - 0.5 + 4.95 * t)
val b = (0.25 / vis) * (x - 0.5 + 0.75 * t)
val c = (0.5 / vis) * (x - 0.375)
val ea = exp(-a)
val eb = exp(-b)
val ec = exp(-c)
return (0.1 * ea + 0.5 * eb + ec) / (ea + eb + ec)
}
}The View
Next to the model, the view is similarly isolated from the other software components. In particular, it has no direct knowledge of the model implementation. This is important from a code reuse point of view. For example, it would be quite easy to use this view for another model by just changing a few text labels.
I’m using TornadoFX to build the interface. Without further explanations of the code, I think you can see how the declarative statements below result in the interfaces shown in Figures 1 and 2.
package view
import controller.ViewController
import javafx.geometry.Pos
import javafx.scene.chart.NumberAxis
import tornadofx.*
var viewController = find(ViewController::class)
class MainView: View() {
override val root = borderpane {
left = vbox {
alignment = Pos.CENTER_LEFT
button("Run Simulation") {
action {
viewController.runSimulation()
}
}
button("Pause Simulation") {
action {
viewController.pauseSimulation()
}
}
button("Resume Simulation") {
action {
viewController.resumeSimulation()
}
}
combobox(viewController.selectedDiscretizer, viewController.dicretizers)
combobox(viewController.selectedStepController, viewController.stepControllers)
label(" Initial StepSize:")
textfield(viewController.initStepSize)
label(" Number of grid points:")
textfield(viewController.nGridPoints)
label(" Model Parameter, viscosity:")
textfield(viewController.viscosity)
label(" UI update delay (ms):")
label("1000=Slow updates, 1=Fast")
textfield(viewController.simulator.sliderValue)
slider(min=1, max=1000, value = viewController.simulator.sliderValue.value) {
bind(viewController.simulator.sliderValue)
}
}
center = tabpane {
tab("Profile Chart 1") {
scatterchart("Burgers' Equation", NumberAxis(), NumberAxis()) {
xAxis.isAutoRanging = false
val xa = xAxis as NumberAxis
xa.lowerBound = 0.0
xa.upperBound = 1.0
xa.label = "x"
yAxis.isAutoRanging = false
val ya = yAxis as NumberAxis
ya.lowerBound = 0.0
ya.upperBound = 1.2
ya.label = "u(x,t)"
series("uSeries") {
data = viewController.uSeriesData
}
series("uAnalSeries") {
data = viewController.uAnalSeriesData
}
}
}
tab("Profile Chart 2") {
linechart("Burgers' Equation", NumberAxis(), NumberAxis()) {
xAxis.isAutoRanging = false
val xa = xAxis as NumberAxis
xa.lowerBound = 0.0
xa.upperBound = 1.0
xa.label = "Time, t"
yAxis.isAutoRanging = false
val ya = yAxis as NumberAxis
ya.lowerBound = 0.0
ya.upperBound = 1.2
ya.label = "u(t)"
series("midGridpoint") {
data = viewController.midGridpointData
}
series("lowGridpoint") {
data = viewController.lowGridpointData
}
series("hiGridpoint") {
data = viewController.hiGridpointData
}
}
}
}
}
}A couple of important comments on the view code:
- There is no explicit mention of any of the UI classes like Button, Label, TextField etc.. Instead, these are created implicitly from TornadoFX’s builder functions.
- There is no procedural code in the view, only configuration statements.
- Values in and out of the interface go through the viewController. The controller is injected into the view by the statement var viewController = find(ViewController::class)
- The view component values and the viewController variables are connected through bindings. Bindings allow for automatic transfer of updated information without having to write code to detect changes and transfer new values from one object to another.
Anyone who has worked with Java/Swing or Java/JavaFX will appreciate how simple it is to build an interface with Kotlin/TornadoFX.
View – Styling
While it is possible to provide styling code directly into the view functions I find that view code becomes less clear. An alternative that I like is to list the styling attributes in a separate Stylesheet class. This is what I used for the example application:
package app
import javafx.scene.paint.Color
import javafx.scene.text.FontWeight
import tornadofx.*
class Styles : Stylesheet() {
init {
button {
padding = box(10.px)
textFill = c("green")
and(hover) {
backgroundColor += Color.AQUAMARINE
}
}
label {
padding = box(5.px)
fontSize = 14.px
fontWeight = FontWeight.BOLD
textFill = c("blue")
}
}
}I have only done the most basic of what you can achieve with these Stylesheets. For example, I specify how much padding the buttons should have and their text color. I also specify the desired color change when the mouse “hovers” over them. Similar decorations for the labels are also shown.
The Controller
The controller usually takes a very central position in most MVC designs. In my version it owns the model and it is injected into the view as I mentioned above. The controller is also an Observer of the Simulator (see below). As such it implements the IObserver‘s update(…) function. This function is called from the Simulator when changes in the model’s data have taken place and need to be displayed. Recall that the model does not know about the view and therefore has no direct way of communicating with it. All communication between the model and the view must pass through the controller.
The controller implements a few JavaFX and TornadoFX data structures that are observable to view items through bindings. For example, take the uSeriesData in the controller. It holds data for one of the series in the view’s Profile Chart 1. This is how we use it in the view:
series("uSeries") {
data = viewController.uSeriesData
}In the controller this variable is a special ArrayList and is declared as follows:
var uSeriesData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()When the Simulator sends the controller an update(…) request, the uSeriesData array is updated based on information it finds in the model.
if (updateCounter > updateFrequency || updateCounter == 0) {
for (i in 0 until model.nGridPoints) {
val xValue = model.x[i]
uSeriesData.add(XYChart.Data(xValue, model.u[i]))
}
updateCounter = 1
}The neat feature about these data structures is that they are “observable” in the sense that the chart updates automatically as soon as the controller makes new data available in the uSeriesData array. Similarly, when data items are removed from the array, the display changes accordingly. In other words, there is no need to explicitly “refresh” the charts with user code. Ref 3. is a good source to learn about these data structures and their use in JavaFX/TornadoFX applications.
package controller
import utilities.IObserver
import javafx.beans.property.SimpleDoubleProperty
import javafx.beans.property.SimpleIntegerProperty
import javafx.beans.property.SimpleStringProperty
import javafx.collections.FXCollections
import javafx.scene.chart.XYChart
import model.BurgersEquation
import model.Simulator
import tornadofx.*
class ViewController: Controller(), IObserver {
var model = BurgersEquation(201)
var endTime = 1.0
var simulator = Simulator(model)
var uSeriesData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()
var uAnalSeriesData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()
var midGridpointData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()
var lowGridpointData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()
var hiGridpointData = FXCollections.observableArrayList<XYChart.Data<Number, Number>>()
val dicretizers = FXCollections.observableArrayList("Euler", "RungeKutta", "RKFehlberg")
val stepControllers = FXCollections.observableArrayList("FixedStep", "VariableStep")
val selectedDiscretizer = SimpleStringProperty("Euler")
val selectedStepController = SimpleStringProperty("FixedStep")
val initStepSize = SimpleDoubleProperty(0.001)
val nGridPoints = SimpleIntegerProperty(model.nGridPoints)
val viscosity = SimpleDoubleProperty(model.vis)
var updateCounter = 0
val updateFrequency = 4
init {
simulator.addIObserver(this)
}
fun runSimulation() {
model = BurgersEquation(nGridPoints.value)
model.vis = viscosity.value
simulator.ode = model
simulator.discretizer = selectedDiscretizer.value
simulator.stepSizeType = selectedStepController.value
simulator.initialStepSize = initStepSize.value
simulator.runSimulation()
}
fun pauseSimulation() {
simulator.pauseSimulation()
}
fun resumeSimulation() {
simulator.resumeSimulation()
}
override fun update(theObserved: Any?, changeCode: Any?) {
val code = changeCode as String
when (code) {
"reset" -> {
if (uSeriesData.size > 1) {
uSeriesData.remove(0, uSeriesData.size)
uAnalSeriesData.remove(0, uAnalSeriesData.size)
midGridpointData.remove(0, midGridpointData.size)
lowGridpointData.remove(0, lowGridpointData.size)
hiGridpointData.remove(0, hiGridpointData.size)
}
}
else -> {
val time = model.time
if (updateCounter > updateFrequency || updateCounter == 0) {
for (i in 0 until model.nGridPoints) {
val xValue = model.x[i]
uSeriesData.add(XYChart.Data(xValue, model.u[i]))
uAnalSeriesData.add(XYChart.Data(xValue, model.phi(x = xValue, t = time)))
}
updateCounter = 1
}
updateCounter += 1
val midGridpoint = model.nGridPoints / 2
val lowGridpoint = midGridpoint - 20 * model.nGridPoints / 201
val hiGridpoint = midGridpoint + 20 * model.nGridPoints / 201
midGridpointData.add(XYChart.Data(time, model.u[midGridpoint]))
lowGridpointData.add(XYChart.Data(time, model.u[lowGridpoint]))
hiGridpointData.add(XYChart.Data(time, model.u[hiGridpoint]))
}
}
}
}There are a few more modules we have to discuss before the app is complete. One of these is the Simulator.
The Simulator
This module is most closely characterized as a model but it is generic enough that it can be treated separately. The simulator is responsible for the numerical integration and for notifying the controller when is time to sample the model for new data to display.
The simulator is generic in the sense that it can integrate any model as long as the model implements the Integratable interface. The simulator itself implements the interface IObservable which means that it can keep track of, and notify, observing objects (e.g. the controller).
An important task for the simulator is to start the integration and run it to completion without blocking the user from working with the UI. Traditionally this is done by starting a low priority background Thread. However, threads can be tricky to work with, especially around shared data. Instead I have opted to use Kotlin’s Coroutine package. Ref. 4 is the perfect source to learn about coroutines. Here I will only highlight the features I have used.
Coroutines are launched in a CoroutineScope. For UI applications it is quite useful to derive a private scope from the general CoroutineScope() but specify that we want the coroutine to be dispatched on the JavaFx UI thread.
import kotlinx.coroutines.*
import kotlinx.coroutines.javafx.JavaFx
class Simulator(var ode: Integratable) : IObservable {
private var job = Job()
private val myScope: CoroutineScope = CoroutineScope(Dispatchers.JavaFx + job)
:
:
:
}We use the private scope to launch a coroutine with code provided in the trailing lambda.
myScope.launch {
while (time <= endTime) {
time = integrator.currentTime
integrator.startTime = time
integrator.endTime = time + dt
integrator.continueCalculations()
:
:
:
}
}You can easily identify these code snippets in their complete context of the Simulator code below. The coroutines are quite nice for dynamic simulations like this because we can implement start, stop, pause, resume, etc. without freezing the UI or making it sluggish.
package model
import integrators.DiscretizationModel
import integrators.Integratable
import integrators.IntegrationServer
import integrators.StepSizeControlModel
import javafx.beans.property.SimpleDoubleProperty
import utilities.IObservable
import utilities.IObserver
import utilities.ObservableComponent
import kotlinx.coroutines.*
import kotlinx.coroutines.javafx.JavaFx
class Simulator(var ode: Integratable) : IObservable {
private val myObservableComponent: ObservableComponent = ObservableComponent()
private var job = Job()
private val myScope: CoroutineScope = CoroutineScope(Dispatchers.JavaFx + job)
val sliderValue = SimpleDoubleProperty(200.0)
var sliderValueInt: Long = 200
lateinit var integrator: IntegrationServer
var discretizer = "Euler"
var stepSizeType = "FixedStep"
lateinit var discretizationType: DiscretizationModel
lateinit var stepSizeControlType: StepSizeControlModel
var time = 0.0
var endTime = 1.0
var reportingInterval = 0.1
var dt = reportingInterval / 10
var dt0 = dt
var initialStepSize = 0.001
var simulationPaused = false
var endSimulation = false
private var reportTimer = 0.0
var x: DoubleArray
init {
val dim = ode.dimension()
x = DoubleArray(dim)
System.arraycopy(ode.initialConditionsUsingArray(x), 0, x, 0, dim)
}
fun reset() {
discretizationType = when(discretizer) {
"RungeKutta" -> DiscretizationModel.ClassicalRK
"RKFehlberg" -> DiscretizationModel.RKFehlberg
else -> DiscretizationModel.ModifiedEuler
}
stepSizeControlType = when(stepSizeType) {
"VariableStep" -> StepSizeControlModel.VariableStepController
else -> StepSizeControlModel.FixedStepController
}
x = DoubleArray(ode.dimension())
System.arraycopy(ode.initialConditionsUsingArray(x), 0, x, 0, ode.dimension())
integrator = IntegrationServer(discretizationType, stepSizeControlType);
integrator.ode = ode
integrator.initialStepSize = initialStepSize
integrator.accuracy = 1.0e-5
reportingInterval = 0.03
dt = reportingInterval / 2
dt0 = dt
time = 0.0
reportTimer = 0.0
integrator.startTime = 0.0
integrator.start(x)
}
fun pauseSimulation() {
simulationPaused = true
}
fun resumeSimulation() {
simulationPaused = false
}
fun endSimulation() {
endSimulation = true
}
fun runSimulation() {
reset()
endSimulation = false
simulationPaused = false
myScope.launch {
myObservableComponent.notifyIObservers(this, "reset")
while (time <= endTime) {
time = integrator.currentTime
integrator.startTime = time
integrator.endTime = time + dt
integrator.continueCalculations()
time = integrator.currentTime
x = integrator.currentValues()
reportTimer += dt
dt = if (simulationPaused) {
delay(500L)
0.0
} else {
dt0
}
if (reportTimer >= reportingInterval) {
sliderValueInt = sliderValue.value.toLong()
delay(sliderValueInt)
myObservableComponent.notifyIObservers(this, "update")
reportTimer = 0.0
}
if (time >= endTime || endSimulation) {
myObservableComponent.notifyIObservers(this, "done")
}
}
}
}
override fun addIObserver(anIObserver: IObserver?) {
myObservableComponent.addIObserver(anIObserver)
}
override fun deleteIObserver(anIObserver: IObserver?) {
myObservableComponent.deleteIObserver(anIObserver)
}
override fun deleteIObservers() {
myObservableComponent.deleteIObservers()
}
}The App
We now have all the pieces ready for the App itself. It is trivially simple as you can see from the code below:
package app
import javafx.stage.Stage
import tornadofx.*
import view.MainView
class MyApp: App(MainView::class, Styles::class) {
override fun start(stage: Stage) {
with(stage) {
width = 1000.0
height = 600.0
}
super.start(stage)
}
}Let’s review what happens here.
- The Application is instantiated along with the View and Styles classes.
- We set the size of the stage (=application window) and start the UI Thread.
- The View instantiates the ViewController, which in turn instantiates a copy of the Model and the Simulator.
At that point all the actors are on stage, so to speak, and the application is ready for user input. In the short video below I show how the app is used.
Conclusions
Kotlin is a perfect tool for dynamic simulations because it multi-platform (by virtue of running on the JVM) and fast. TornadoFX, a domain specific language written in Kotlin for use with JavaFX, is also quite attractive in constructing a user interface quickly and with minimal code.
References
- W. E. Schiesser, Computational Mathematics in Engineering and Applied Science, CRC Press, 1994.
- W. E. Schiesser, Spline Collocation Methods for Partial Differential Equations, John Wiley & Sons, 2017.
- K. Sharan and P. Späth, Learn JavaFX 17 2nd ed., Apress Media LLC, 2022.
- M. Moskala, Kotlin Coroutines, Kt. Academy, 2022